Московская Сретенская Духовная Академия
Почему Пасху отмечают каждый год в разные дни: о появлении первых праздничных календарей
2 мая 2019
Деятельность
Почему Пасху отмечают каждый год в разные дни: о появлении первых праздничных календарей
Пасхалия ― метод расчета, позволяющий определить даты празднования Пасхи и переходящих церковных праздников по специальным таблицам, в которых определяется взаимосвязь календарно-астрономических величин. Вследствие этого составляется календарь праздников. Но тогда возникает закономерный вопрос: кто этим занимался и как все начиналось? Ведь даже сейчас христиане используют разные календари: юлианский и григорианский.  Содержание:
Содержание:
До начала III века многие христиане праздновали Пасху, сообразуясь с Пасхой иудеев. Впоследствии Римская и Александрийская Церкви разработали собственные пасхалии — методы расчета даты Пасхи, независимые от иудейской традиции. Эти две пасхалии во многом были схожи, но имели и различия, ввиду которых две эти Церкви нередко праздновали Пасху в разные дни.
На Первом Вселенском Соборе в Никее были приняты постановления относительно празднования Пасхи, текст которых не сохранился. Из косвенных источников можно уяснить, что суть этих постановлений ― праздновать Пасху всем христианам в один и тот же день и не отмечать ее вместе с иудеями, у которых рассчитанная дата Пасхи иногда стала приходиться на период до весеннего равноденствия.
Тем не менее, даже после Никейского Собора разные Церкви периодически праздновали Пасху не в один принятый день. Это было связано с тем, что как Александрийская, так и Римская Церкви по-прежнему держались каждая своей пасхалии. Однако с течением времени Римская Церковь постепенно отказывается от тех положений своей пасхалии, которые отличаются от таковых в александрийской пасхалии. В VI веке Римская Церковь полностью переходит на пасхалию Александрии, но римская пасхалия еще удерживается на отдаленных окраинах запада. Только к началу IX века Вселенская Церковь стала следовать александрийской пасхалии и, соответственно, праздновать Пасху в один и тот же день.
В основу лунно-солнечных календарей полагается тропический год — промежуток времени между двумя последовательными прохождениями центра диска Солнца через точку весеннего равноденствия

Для понимания математических основ пасхалии необходимо уяснить принцип устройства лунно-солнечных и солнечных календарей, история которых представлена в многочисленных учебных пособиях и справочниках[1].
Лунно-солнечный календарь
Календарем принято называть определенную систему счета продолжительных промежутков времени с подразделениями их на отдельные, более короткие периоды — годы, месяцы, недели, дни[2].
Лунно-солнечный календарь[3] характерен тем, что используется для привязки времен года к определенным месяцам календарного года и для привязки фаз Луны (новолуния, первой четверти, полнолуния и последней четверти) к определенным числам (дням) календарного месяца.
Изменение фаз Луны связано с освещением ее Солнцем во время обращения вокруг Земли — за один полный оборот. За это время Луна проходит все четыре указанные фазы. Период такого обращения называется синодическим месяцем и, согласно современным подсчетам, составляет (в среднем) 29,53058812 суток[4].
Смена времен года связана с обращением Земли вокруг Солнца. Существуют разные способы определения периода полного обращения Земли вокруг Солнца. В основу лунно-солнечных календарей полагается тропический год — промежуток времени между двумя последовательными прохождениями центра диска Солнца через точку весеннего равноденствия. Не углубляясь в определение термина точка весеннего равноденствия, можно обозначить ее как некоторую точку на небе, определяемую по звездам. Прохождение Солнца через эту точку связано с днем весеннего равноденствия (или просто весенним равноденствием) — земным днем, характеризующимся равенством продолжительности дня и ночи. Длительность тропического года составляет 365,24219880 суток[5].
Как видно, длительность синодического месяца не выражается целым числом суток, поэтому при разработке лунно-солнечного календаря необходимо вводить календарные месяцы длительностью по 29 и 30 суток с их чередованием, чтобы в среднем длительность календарного месяца совпадала с длительностью синодического месяца. При таком подходе полнолуние всегда будет выпадать на 14-е число месяца.
Длительность тропического года тоже не совпадает с целым числом синодических месяцев:
12 синодич. мес. ≈ 354d,367,
13 синодич. мес. ≈ 383d,898.
Поэтому при разработке календаря также необходимо вводить календарные годы различной длины: 12 месяцев (обычные или простые годы) и 13 месяцев (эмболимические или эмболисмические годы), чтобы средняя длительность календарного года была равна длительности тропического года. В этом случае времена года будут приходиться на одни и те же месяцы календарного года (см. рис. 1).
Вставка (интеркаляция) дополнительного, тринадцатого месяца в календарный год может быть основана на непосредственных наблюдениях, как это было, например, в иудейском календаре до разрушения второго храма, или же на повторяющемся цикле из N лет, среди которых M лет — эмболимические, а оставшиеся (N— M) — простые.
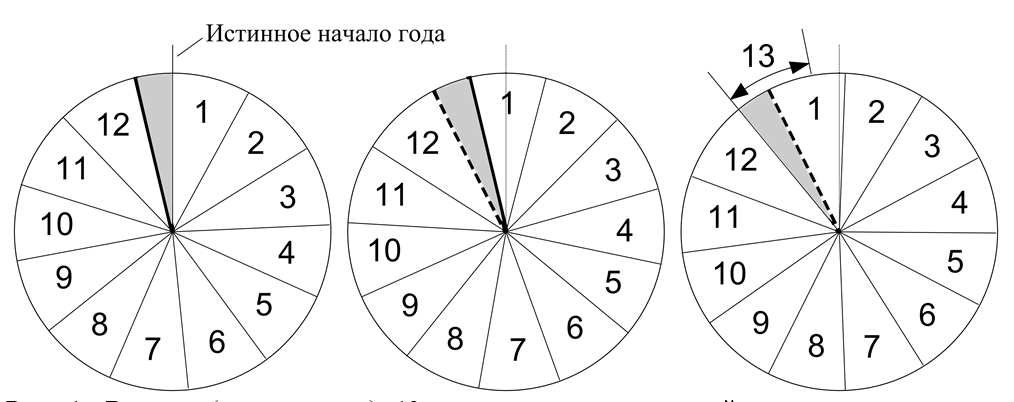
Примером такого цикла является 19-летний цикл (N = 19), разработанный древнегреческим астрономом Метоном в 432 г. до н.э.[6] В этом цикле содержится ровно 235 месяцев, то есть первый день первого месяца совпадает с первым днем первого года в цикле, а последний день 235-го месяца — с последним днем 19-го года. Ввиду того, что в цикле должно быть целое число суток, а
19 тропич. лет ≈ 6939d,602 и
235 синодич. мес. ≈ 6939d,688,
число суток в метоновом цикле полагается равным 6940.
Количество эмболимических лет в цикле Метона равно семи (М = 7), поскольку 7 (эмболимич. лет) × 13 (мес.) + 12 (простых лет) × 12 (мес.) = 235 (мес.). Ввиду того, что 6940d = 125 × 30d + 110 × 29d, 30-дневных календарных месяцев в цикле Метона на 15 больше, чем 29-дневных.
Солнечный календарь
В отличие от лунно-солнечного календаря, солнечный календарь[7] используется лишь для привязки времен года к определенным месяцам календарного года, привязка солнечного календаря к фазам Луны не делается.
Независимость от фаз Луны позволяет вводить календарные месяцы произвольной длины. Поэтому календарный год уже не должен содержать целое число синодических месяцев, а лишь целое число суток. Длительность тропического года не выражается целым числом суток, поэтому при разработке календаря необходимо вводить обычные и високосные годы длительностью по 365 и 366 суток соответственно.
Широко известен юлианский календарь, разработанный группой александрийских астрономов и введенный в употребление в Римской республике Гаем Юлием Цезарем в 45 г. до Р.Х. В нем високосным считается каждый четвертый год, следовательно средняя длительность года составляет (3 (обычных года) × 365d + 1 (високосный год) × 366d) / 4 = 365,25d, что является хорошим приближением длительности тропического года. Период времени длительностью 365,25 суток называется юлианским годом. В современной России юлианский календарь называют старым стилем.
Новым же стилем называется григорианский календарь, который является более точным в отношении тропического года, чем юлианский. Единственное отличие григорианского календаря от юлианского состоит в том, что правило для определения високосного года несколько усложняется: високосными являются те годы, номера которых делятся на 4, но не делятся на 100; однако, если номер года делится на 400, то год считается високосным. Это различие приводит к тому, что юлианские даты отстают от григорианских. На данный момент это отставание составляет 13 дней.
Необходимо отметить, что в солнечных календарях происходит не только привязка времен года к определенным календарным месяцам, но и привязка таких ежегодных событий, как, например, равноденствие (весеннее и осеннее), к определенному календарному дню.
Период времени длительностью 365,25 суток называется юлианским годом ― в современной России юлианский календарь называют старым стилем

Так, в классической александрийской пасхалии днем весеннего равноденствия полагается 21 марта юлианского календаря (подробнее об этом будет сказано ниже).
|
№ месяца |
Александрийский календарь |
Юлианский календарь |
|
1 |
1 тота |
29 (30) августа |
|
2 |
1 фаофи |
28 (29) сентября |
|
3 |
1 атира |
28 (29) октября |
|
4 |
1 хойяка |
27 (28) ноября |
|
5 |
1 тиби |
27 (28) декабря |
|
6 |
1 мехира |
26 (27) января |
|
7 |
1 фаменота |
25 (26) февраля |
|
8 |
1 фармути |
27 марта |
|
9 |
1 пахона |
26 апреля |
|
10 |
1 пайни |
26 мая |
|
11 |
1 эпифи |
25 июня |
|
12 |
1 месори |
25 июля |
|
|
1 эпагомен |
24 августа |
|
|
(6 эпагомен) |
(29 августа) |
Александрийский солнечный календарь был введен в Египте императором Октавианом Августом в 25 году до Р.Х.[8] Александрийский календарь основан на древнеегипетском гражданском солнечном календаре, в котором календарный год состоит из 12 месяцев по 30 суток каждый и 5 дополнительных суток (эпагомен), идущих в конце года. Таким образом, длина календарного года в Древнем Египте составляла 365 суток.
Император Октавиан реформировал древнеегипетский календарь, включив в него високосные годы по 366 суток на манер юлианского календаря: каждый четвертый год стал считаться високосным. Високосные годы стали содержать 6 эпагомен вместо 5. Для удобства високосные годы александрийского календаря непосредственно предшествовали високосным годам юлианского календаря. Начало александрийского года, 1 тота, совпадает с 29 августа юлианского года (см. таблицу выше). Соответственно, 2 тота — это 30 августа и т. д. Если же александрийский год является високосным, то 29 августа соответствует 6-му эпагомену, 1 тота следующего года смещается на 30 августа, 2 тота — на 31 августа и т. д. Однако уже через полгода это смещение на один день устраняется, поскольку в конце февраля происходит вставка дополнительного дня (29 февраля) в юлианский високосный год, который следует за александрийским високосным. После этого, 5 фаменота будет как обычно соответствовать 1 марта, 6 фаменота — 2 марта, …, 30 фаменота — 26 марта, 1 фармути — 27 марта и т.д.
Что касается нумерации лет, то александрийский календарь отстает от римского на 9 месяцев. Так, например, 1 тота 322 года по александрийскому календарю приходится на 29 августа 322 года по римскому.
Лунно-солнечные календари, основанные на циклах
Здесь описываются лишь те лунно-солнечные календари, которые использовались в христианских и иудейских пасхалиях.
Интеркаляция (вставка) тринадцатого месяца в календарный год на основе повторяющегося цикла имеет преимущество в том, что отпадает необходимость непосредственных наблюдений за Солнцем или природными явлениями. Для того, чтобы создать хороший цикл, необходимо подобрать такое количество тропических лет и такое количество синодических месяцев, чтобы количество суток в них совпадало с хорошей степенью точности.
Например, в рассмотренном выше цикле Метона взято 19 тропических лет и 235 синодических месяцев. Но методы такого подбора выходят за рамки данной статьи.
Недостаток использования циклов состоит в том, что достигнуть абсолютной точности в подборе количества тропических лет и синодических месяцев невозможно. Следовательно, неизбежны расхождения лунно-солнечного календаря, основанного на цикле, с Солнцем и Луной. Другими словами, привязка времен года к определенным месяцам календарного года и привязка фаз Луны к определенным числам (дням) календарного месяца будет все больше и больше ослабевать с течением времени.
19-летний цикл и циклы на его основе
Цикл Метона
Как уже было сказано, 19-летний цикл разработал древнегреческий астроном Метон в 432 году до Р.Х. Аналогичный 19-летний цикл использовался в Древнем Вавилоне с IV веке до Р.Х. (по некотором данным — с VI веке до Р.Х.)[9]. Он был открыт и в Древнем Китае, примерно в VI веке до Р.Х., и широко использовался среди народов Дальнего Востока и евразийских степей.
Выше уже были подсчитаны основные параметры этого цикла. Расхождения, которые дает этот цикл с Солнцем и с Луной за один цикл:
Привязка времен года к определенным месяцам календарного года и привязка фаз Луны к определенным числам (дням) календарного месяца будет все больше и больше ослабевать с течением времени

с Солнцем: 6940d — 19 (тропич. лет) × 365d,24219880 = 0d,3982228,
с Луной: 6940d — 235 (синодич. мес.) × 29d,53058812 = 0d,3117918.
Следовательно, расхождение в 1 сутки с Солнцем будет накапливаться каждые (19 / 0,3982228 ≈) 48 лет, а с Луной — каждый (19 / 0,3117918 ≈) 61 год. Как видно, расхождения будут иметь характер «отставания» календаря от Солнца и от Луны.
В нижеследующей таблице приведены все параметры метонова цикла:
|
Число лет в цикле |
19 |
|
Число эмболимических лет |
7 |
|
Число 29-дневных календ. мес. |
110 |
|
Число 30-дневных календ. мес. |
125 |
|
Специальные корректировки |
— |
|
Число суток в цикле |
6940 |
|
Расхождение в 1 сутки (с Солнцем) |
≈ каждые 48 лет (отставание) |
|
Расхождение в 1 сутки (с Луной) |
≈ каждый 61 год (отставание) |
Для использования цикла Метона (как и циклов Каллиппа и Гиппарха, описываемых ниже) на практике необходимо:
1) определить номера эмболимических годов;
2) фиксировать начало отсчета цикла — дату, от которой будут отсчитываться календарные дни;
3) определить, какие именно месяцы будут 29-дневными, а какие — 30-дневными.
Цикл Каллиппа
В IV веке до Р.Х. древнегреческий астроном Каллипп усовершенствовал цикл Метона, создав свой 76-летний цикл. Аналогичный цикл был известен в Восточной Азии, не позднее IV века до Р.Х.
Суть усовершенствования состоит в том, что каждые 76 лет, то есть каждые четыре 19-летних метоновых цикла в календаре, исключается один день[10],[11]. Эта корректировка уменьшает расхождение календаря с Солнцем и с Луной. Соответственно, цикл Каллиппа можно рассматривать или как 19-летний цикл со специальными корректировками (поправкой по Каллиппу), или как (19 × 4 =) 76-летний цикл без корректировок:
|
|
Как 19-летний цикл |
Как 76-летний цикл |
|
|
Число лет в цикле |
19 |
× 4 |
= 76 |
|
Число эмболимических лет |
7 |
= 28 |
|
|
Число 29-дневных календ. мес.* |
110 |
+ 1 = 441 |
|
|
Число 30-дневных календ. мес.* |
125 |
– 1 = 499 |
|
|
Специальные корректировки |
Исключение дня в 30-дневном календ. мес. — 1 раз каждые 76 лет (т.е. каждые 4 цикла) |
— |
|
|
Число суток в цикле |
6939,75 (в среднем) |
× 4 |
= 27759 |
|
Погрешность в 1 сутки (по Солнцу) |
≈ каждые 128 лет (отставание) |
||
|
Погрешность в 1 сутки (по Луне) |
≈ каждые 307 лет (отставание) |
||
* здесь и далее: без учета специальных корректировок.
Цикл Гиппарха
В 125 году до Р.Х. греческий астроном Гиппарх создал новый цикл, усовершенствовав цикл Каллиппа путем исключения одного календарного дня каждые 304 года, то есть каждые четыре 76-летних цикла Каллиппа. Это усовершенствование уменьшает расхождение календаря с Солнцем и с Луной. Расхождение с Луной становится небольшим, но при этом оно приобретает характер обгона. Как видно, цикл Гиппарха можно рассматривать или как 19-летний, или 76-летний цикл со специальными корректировками (поправкой по Гиппарху), или как (76 × 4 =) 304-летний цикл без корректировок:
|
|
Как 19-летний цикл |
Как 76-летний цикл |
Как 304-летний цикл |
||
|
Число лет в цикле |
19 |
× 4 |
= 76 |
× 4 |
= 304 |
|
Число эмболимических лет |
7 |
= 28 |
= 112 |
||
|
Число 29-дневных календ. мес. |
110 |
+ 1 = 441 |
+ 1 = 1765 |
||
|
Число 30-дневных календ. мес. |
125 |
– 1 = 499 |
– 1 = 1995 |
||
|
Специальные корректировки |
Исключение дня в 30-дневном календ. мес. — 5 раз каждые 304 года (т.е. 5 раз каждые 16 циклов) |
Исключение дня в 30-дневном календ. мес. — 1 раз каждые 304 года (т.е. 1 раз каждые 4 цикла) |
— |
||
|
Число суток в цикле |
6939,6875 (в среднем) |
× 4 |
= 27758,75 (в среднем) |
× 4 |
= 111035 |
|
Погрешность в 1 сутки (по Солнцу) |
≈ каждые 222 года(отставание) |
||||
|
Погрешность в 1 сутки (по Луне) |
≈ каждые 26829 лет (обгон) |
||||
Юлианский 19-летний (76-летний) цикл
Особым этапом в развитии лунно-солнечных календарей стало совмещение лунно-солнечного календаря, основанного на 19-летнем цикле, с юлианским солнечным календарем. Получившийся 19-летний цикл носит название юлианского[12] и был создан для удобства расчета даты Пасхи. Впервые юлианский цикл встречается в пасхалии еп. Анатолия Лаодикийского (277 год по Р.Х.). Тем не менее, возможно, что подобный цикл появился и раньше, в Сирии.
Суть юлианского цикла состоит в том, что он содержит в себе ровно 19 юлианских годов, то есть (365d,25 × 19 =) 6939d,75. Таким образом, через каждые 19 лет все даты соответствующего лунно-солнечного календаря будут совпадать с датами юлианского календаря. Количество суток в юлианском цикле совпадает с таковым в цикле Каллиппа, поэтому точность этих циклов одинакова.
Дробное количество суток в цикле (6939,75) достигается следующим образом: среди обычных (не вставных) 12-ти календарных месяцев в одном годе цикла содержится шесть 29-дневных и шесть 30-дневных: первый месяц содержит 30 дней, второй — 29, третий — 30 и т.д. Вставные (тринадцатые) же месяцы содержат по 30 дней. Кроме того, вставные дни юлианского календаря (29 февраля) включаются и в соответствующие месяцы лунно-солнечного календаря, образуя 30-дневные или 31-дневные календарные месяцы. Ввиду того, что 19 не кратно 4, вставных дней в 19-летнем цикле бывает либо 4, либо 5. В среднем же в один цикл вставляется (19 / 4 =) 4,75 суток.
Таким образом, общее количество суток в цикле выходит равным ((29d × 6 (мес.) + 30d × 6 (мес.)) × 19 (лет) + 30d× 7 (вставных мес.) + 4,75d =) 6940d,75, что на 1 сутки больше, чем 19 юлианских лет. «Лишние» сутки вычитаются из цикла с помощью так называемого «скачка луны» (saltuslunae) — пропуска одного из дней некоторого месяца.
Особым этапом в развитии лунно-солнечных календарей стало совмещение лунно-солнечного календаря, основанного на 19-летнем цикле, с юлианским солнечным календарем

Количество дней в юлианском цикле чередуется: либо 6939, либо 6940, в зависимости от количества вставочных дней. Включение в лунно-солнечный календарь дополнительных дней, соответствующих 29 февраля юлианского календаря, как бы абстрагирует его от вставок дополнительных дней в солнечный (юлианский) календарь. Именно это обеспечивает тот факт, что каждые 19 лет все даты лунно-солнечного календаря совпадают с датами юлианского календаря, вне зависимости от того, сколько дополнительных дней было добавлено в лунно-солнечный календарь за эти 19 лет.
В нижеследующей таблице приведены все параметры юлианского цикла:
|
|
Как 19-летний цикл |
Как 76-летний цикл |
|
|
Число лет в цикле |
19 |
× 4 |
= 76 |
|
Число эмболимических лет |
7 |
= 28 |
|
|
Число 29-дневных календ. мес. |
(19 × 6 =) 114 |
= 456 |
|
|
Число 30-дневных календ. мес. |
(19 × 6 + 7 =) 121 |
= 484 |
|
|
Специальные корректировки |
1) Вставка дополнительных дней (соответствующих 29 февраля) — 1 раз каждые 4 года; 2) «Скачок луны» — 1 раз каждые 19 лет (т.е. в каждом 19-летнем или 4 раза в 76-летнем цикле соответственно) |
||
|
Число суток в цикле |
6939,75 (в среднем) |
× 4 |
= 27759 |
|
Погрешность в 1 сутки (по Солнцу) |
≈ каждые 128 лет (отставание) |
||
|
Погрешность в 1 сутки (по Луне) |
≈ каждые 307 лет (отставание) |
||
Для использования юлианского цикла (как и 84-летнего цикла, описываемого ниже) на практике необходимо:
1) определить номера эмболимических годов;
2) фиксировать начало отсчета — дату, от которой будут отсчитываться календарные дни;
3) определить положение «скачка луны».
Другим вариантом совмещения лунно-солнечного и юлианского календаря является 84-летний цикл[13]. Происхождение этого цикла неизвестно, но известно, что он был разработан в III в. специально для римской пасхалии.
Принцип организации 84-летнего цикла такой же, как и у юлианского 19-летнего — вставка дополнительных дней, соответствующих 29 февраля юлианского календаря и «скачки луны», которых в этом цикле шесть. Ввиду того, что 84 кратно 4, количество вставных дней в цикле равно (84 / 4 =) 21.
Остальные параметры 84-летнего цикла см. в таблице:
|
Число лет в цикле |
84 |
|
Число эмболимических лет |
31 |
|
Число 29-дневных календ. мес. |
(84 × 6 =) 504 |
|
Число 30-дневных календ. мес. |
(84 × 6 + 31 =) 535 |
|
Специальные корректировки |
1) Вставка дополнительных дней (соответствующих 29 февраля) — 21 раз; 2) 6 «скачков луны» |
|
Число суток в цикле |
(504 × 29 + 535 × 30 + 21 — 6 =) 30681 |
|
Погрешность в 1 сутки (по Солнцу) |
≈ каждые 128 лет (отставание) |
|
Погрешность в 1 сутки (по Луне) |
≈ каждые 66 лет (обгон) |
Как видно, 84-летний цикл дает такую же погрешность по Солнцу, как и юлианский цикл. Погрешность же по Луне у 84-летнего цикла гораздо больше и имеет характер обгона, что особенно ярко проявится в пасхальном споре относительно 455 года, о чем будет идти речь ниже.
Лунной эпактой (или просто эпактой) называется возраст луны (номер лунного дня) на фиксированный календарный день солнечного года. Совокупность эпакт для всех годов цикла образует эпакты цикла. Если в каждой итерации цикла все даты соответствующего лунно-солнечного календаря будут совпадать с датами солнечного календаря, как это происходит, например, в юлианском 19-летнем и 84-летнем циклах, то, очевидно, эпакты цикла будут одинаковы для каждой итерации цикла.
Так, например, эпакты 84-летнего цикла для 1 января таковы: 1, 12, 23, 4, 15, 26, 7, … Характерно, что эпакта с каждым годом возрастает на 11. В случае превышения числа 30, эпакта, соответственно, уменьшается на 30. Если же в цикле присутствует «скачок луны», то в этом месте эпакта увеличивается на 12. На основании этого факта легко определить положение «скачков луны», если известны эпакты цикла.
Необходимо отметить, что правило возрастания эпакт на 11 соблюдается лишь в том случае, если между двумя соседними датами, для которых вычисляется возраст луны, всегда содержится 6 календарных лунных месяцев по 29 дней. Иначе эпакты окажутся «смазанными» ― правило увеличения на 11 не будет выполняться. Например, для 84-летнего цикла эпакты для 15 апреля будут «смазаны».
Чтец Михаил Петрухно
Выпускник Сретенской духовной семинарии
Материал опубликован 02.04.2018 г.
Ключевые слова: пасхалия, система, лунно-солнечный календарь, Рим, Александрия, юлианский календарь, цикл, дата Пасхи, Солнце, Луна, эпакты
[1] См., например, Иванова Н.П., Цыб С.В. Историческая хронология: Курс лекций. Барнаул: Изд-во Алтайского ун-та. — 2003. Каменцева Е.И. Хронология. — 2-е изд., испр. и дополн. — М.: Аспект Пресс. — 2003. Климишин И.А. Календарь и хронология. — 2-е изд., перераб. и доп. — М.: Наука. Главная редакция физ.-мат. лит., 1985. — С. 7. Пронштейн А.П., Кияшко В.Я. Хронология: Учебное пособие. — М.: Высшая школа. — 1981. Цыбульский В.В. Календари и хронология стран мира. — М.: Просвещение. — 1982.
[2] Климишин И.А. Календарь и хронология. 2-е изд., перераб. и доп. — М.: Наука. Главная редакция физ.-мат. лит., 1985. — С. 7.
[3] Там же. С. 48-50.
[4] Там же. С. 34.
[5] Там же. С. 28-29.
[6] Там же. С. 53.
[7] Там же. С. 54.
[8] Там же. С. 225.
[9] Кузенков П.В. Христианские хронологические системы. — М.: Русский изд. центр им. св. Василия Великого, 2015. — С. 391.
[10] Зелинский А.Н. Конструктивные принципы древнерусского календаря // Календарный вопрос: сборник статей / Ред.-сост. А. Чхартишвили. — М.: Изд. Сретенского монастыря, 2000. — С. 234-278.
[11] Кузенков П.В. Христианские хронологические системы. — М.: Русский изд. центр им. св. Василия Великого, 2015. — С. 392.
[12] Кузенков П.В. Христианские хронологические системы. — М.: Русский изд. центр им. св. Василия Великого, 2015. — С.122-124, 392-393. Климишин И.А. Календарь и хронология. — 3-е изд., перераб. и доп. — М.: Наука. Главная редакция физ.-мат. лит., 1990. — С.117.
[13] Кузенков П.В. Христианские хронологические системы. — М.: Русский изд. центр им. св. Василия Великого, 2015. — С. 116-119, 390.
Автор: Михаил Петрухно
Картинка для анонса: Array
Количество показов: 22536
Теги: